Coherent and Incoherent Addition of Waves

In Young’s double slit experiment, the two slits 0.15 mm apart are illuminated by monochromic light of wavelength 450 nm. The screen is 1.0 m away from the slits.

(a) Find the distance of the second (i) bright fringe, (ii) dark fringe from the central maximum.

Which of the following expressions is/are correct for Young’s experiment?

(i) condition for bright fringes  $x=n\lambda \frac{D}{d}$

(ii) condition for dark fringes  $x=\left(2n-1\right)\frac{\lambda }{2}\frac{D}{d}$

ii) fringe width  $\beta =\frac{\lambda D}{d}$

A point source emits sound equally in all directions in a non-absorbing medium. Two points P and Q are at a distance of 9 metres and 25 metres respectively from the source. The ratio of amplitudes of the waves at P and Q is ___________

A point source emits sound equally in all directions in a non-absorbing medium. Two points P and Q are at a distance of 9 metres and 25 metres respectively from the source. The ratio of amplitudes of the waves at P and Q is ___________

Two beams of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is  $\frac{\pi }{2}$  at point A and  $\pi$ at point B. Then the difference between the resultant intensities at A and B is

A thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown in figure. The observed interference fringes from this combination shall be

Two coherent monochromatic light beams of intensities $\mathrm{I}$ and $\mathrm{4I}$ are superposed. The maximum and minimum possible intensities in the resulting beam are

Two coherent monochromatic light beams of intensities $I$ and $4I$ are superposed. The maximum and minimum possible intensities in the resulting beam are

A single slit of width $a$ is illuminated by a monochromatic light of wavelength $600 \mathrm{nm}$. The value of $a$ for which first minimum appears at $\theta ={30}^{\mathrm{o}}$ on the screen will be :

Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R

Assertion A: The phase difference of two light waves change if they travel through different media having same thickness, but different indices of  refraction.

Reason R: The wavelengths of waves are different in different media.

In the light of the above statements, choose the most appropriate answer from the options given below

A cat is able to see in low light intensity situations by virtue of its large sized pupils of diameter $~16 \mathrm{mm}$ and due to the presence of excess number of cone cells on its retina. They can detect light of intensity $\mathrm{I}$ as low as $~{10}^{-10} \mathrm{W}/{\mathrm{m}}^2$.

If intensity $\mathrm{I}$ of light is defined as energy of radiation times the number of photons per unit area, then determine the minimum number of incident photons per second of wavelength $600 \mathrm{nm}$ that are required in a radiation to be detected by a cat’s eye? Take $hc~ 2\times {10}^{-16} \mathrm{J}-\mathrm{nm}$.

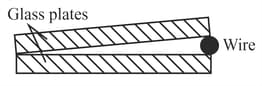
A thin wire is placed between two accurately flat glass plates, creating a wedge of air between the plates. The plates are illuminated with a sodium lamp ($589$ $\mathrm{nm}$) and viewed at near-normal incidence.$80$ bright fringes are counted over the $45.0 \mathrm{mm}$between the line where the plates are touching and the location of the wire.
(i) Sketch the fringe pattern as seen from above the glass plates (i.e. looking down from the top of the diagram above).
(ii) Calculate the diameter of the wire. You must explain your method - don't just plug numbers into an equation Explain why a dark fringe is observed along the line where the plates are touching.
(iii)Explain why a dark fringe is observed along the line where the plates are touching.

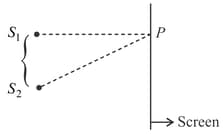
Statement-I: For the situation shown in figure, two identical coherent sources of light produce interference pattern on the screen. The intensity of minima nearest to ${\mathrm{S}}_1$ is not exactly zero.

Statement-Il: Minimum intensity is zero when interfering waves have same intensity at the location of superposition.

​​​​​​​

The interference pattern is obtained with two coherent light sources of intensity ratio $4:1$. And the ratio $\frac{I_{\max }+I_{\min }}{I_{\max }-I_{\min }}$ is $\frac{5}{x}$. Then, the value of $x$ will be equal to :

Two light beams of intensities in the ratio of $9:4$ are allowed to interfere. The ratio of the intensity of maxima and minima will be :

Two coherent sources of light with amplitudes $A_1=A_2=A$ and intensities $I_1=I_2=I$ interferes with each other having phase difference of $\frac{\pi }{3}$. Find resultant amplitude, maximum and minimum amplitude. Also find resultant, maximum and minimum intensity.

Two superimposing waves are represented by equation $y_1=2\sin 2\pi (10t-0.4x)$ and $y_2=4\sin 2\pi (20t-0.8x)$. The ratio of  $I_{\max }$ to $I_{\min }$ is

Waves of wavelength $4 \mathrm{m}$ is generated in a medium. Two points $P$ and $\mathrm{Q}$ are chosen in the direction of propagation with $P$ ahead of $Q$. The instantaneous phase of $P$ is $4\pi$ rad at a certain instant. Find the phase of $Q$ at this instant if separation $PQ$ is $6 \mathrm{m}$

In the diagram shown, the separation between the slit is equal to $3\lambda$, where $\lambda$ is the wavelength of the light incident on the plane of the slits $A$ thin film of thickness $3\lambda$ and refractive index $2$ has been placed in the front of the upper slit. Assuming $D\gg \lambda$ the distance of the zero order maxima (where phase difference between the two interfering waves is zero) on the screen from $O$ is given most appropriately by which of the following options?

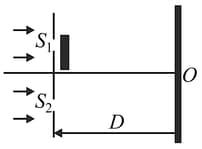
In Young's double-slit interference experiment, the fringe pattern is observed on a screen placed at a distance $D.$ The slits are separated by $d(<<D)$ and are illuminated by coherent sources. The central maxima is formed at the geometrical center on the screen with respect to the slits. If at a distance $h$ from the central maximum on the screen the intensity is half of the maximum intensity then the value of $\lambda$ may be,